
Greenwich Park with the Royal Observatory, on Easter Monday
Image extracted from page 185 of Modern London; being the history and present state of the British Metropolis. Illustrated with numerous copper plates, by Richard Phillip (1804). Original held and digitized by the British Library. Sourced via Wikimedia Commons.
Future Mariners: Astrometry with TMT Part 1
July 10th, 2018
•
TMT Blog
No twilight within the courts of the Sun.
The Sun's rim dips; the stars rush out:
At one stride comes the dark;
With far-heard whisper, o'er the sea,
Off shot the spectre-bark.
At the rising of the Moon,
We listened and looked sideways up!
Fear at my heart, as at a cup,
My life-blood seemed to sip!
The stars were dim, and thick the night,
The steerman's face by his lamp gleamed white;
From the sails the dew did drip—
Till clomb above the eastern bar
The hornéd Moon, with one bright star
Within the nether tip.
-Samuel Taylor Coleridge, The Rime of the Ancient Mariner

The Rime of the Ancient Mariner.
Image Credit: Gustav Doré (1866). Reproduced from Wikipedia Commons/A. Wagner
Introduction
While pursuing my doctorate in experimental astrophysics, in London, I would sometimes visit the map room at the British Museum. I'd look at the ancient maps, with coastlines that were recognizable, but distorted and out of proportion. Some areas were imagined to be populated by terrifying monsters, or even left blank, because cartographers of the time had insufficient information to do better. Over time, as more information was observed or extrapolated, maps became more accurate, and were able to cover more area, piecing together our picture of the world like a puzzle, a little bit at a time. And as we did this, piece by piece, we learned more about our place in the world.
Here’s an example of an old map, showing western Europe’s 1502 limited understanding of what southeast Asia looks like. The map is charmingly inaccurate.
Detail of Asia, from the Cantino Planisphere, which depicts the world as known to the Europeans after the exploration voyages at the end of the fifteenth and beginning of the sixteenth century to the Americas, Africa, and India. Image Credit: Anonymous Portuguese author (1502).
Source: Biblioteca Estense Universitaria, Modena, Italy. Reproduced from Wikipedia Commons.
Astronomers, too, are explorers, trying to map unfamiliar territories. The ancients imagined the stars as celestial hunters and swans and dragons, but by piecing together information bit by bit, astronomers have been able to discover more about what those glowing points in the sky really are, and where they really are, which ultimately tells us more about our place in the cosmos. In this blog entry, I’ll introduce you to astrometry, the science of precisely measuring the positions of astronomical objects and tracking their motions as they traverse the sky. Astrometry will play a central role in much of the science that TMT will pursue.
You Are Here
When we describe the location of something on Earth, we might use landmarks and directions, or provide a street address. Or we can use a two-dimensional coordinate system, specifying the first coordinate as this far away from one axis, and the next coordinate as that far away from a second axis (running in a direction not aligned to the first axis).
We commonly use the coordinate system. One coordinate describes latitude (how far north or south we are), with the equator representing zero degrees latitude. The other describes longitude (how far east or west), with the prime meridian representing zero degrees longitude running through Greenwich in the United Kingdom. Visits to Greenwich for me always included a visit to the Royal Greenwich Observatory, a stroll through Greenwich Park, and a visit to the National Maritime Museum.

Greenwich Park with the Royal Observatory, on Easter Monday
Image extracted from page 185 of Modern London; being the history and present state of the British Metropolis. Illustrated with numerous copper plates, by Richard Phillip (1804). Original held and digitized by the British Library. Sourced via Wikimedia Commons.
Today we can readily determine our geographic location in terms of latitude and longitude, by using GPS. But astonishing as it may be to the legions of teenagers out there, this information wasn't always as close as a glance at our phone. In the days before GPS and smartphones, people could figure out latitude from looking at how high the Sun was in the sky at noontime, and factoring in the day of the year and the corresponding position of the Earth along its orbit around the Sun. Perhaps you've already noticed for yourself that you can estimate your latitude with some intuitive observations: how high the sun goes in the sky; what time of year it is; how long the daylight lasts; and where on the horizon the sun rises and sets.
Longitude was harder, and for centuries, a practicable way to measure it precisely eluded even some of history's greatest minds (including that of Galileo). In the end, the method settled on was for seafarers to carry two clocks, one set to the time at a port of reference, and a second one, which was reset to noon every day when the Sun was at its highest point in the sky. The longitude of the ship could then be calculated from the difference in time between the two clocks—so long as both clocks ran accurately. (Readers familiar with Einstein's special theory of relativity may wonder whether his thinking found inspiration from this practice.) To learn more about the fascinating history of longitude and navigation, I recommend Dava Sobel's Longitude: The True Story of a Lone Genius Who Solved the Greatest Scientific Problem of His Time.
Even today, people at sea learn and practice old celestial navigation methods as a backup to GPS. When I was doing atmospheric, oceanographic and entomological research from the M/V OCEANIC, I saw some beautiful sextants (sextants measure the exact angle of something in the sky compared to the horizon) on the bridge of the ship. The crew explained they had to keep up their training in traditional navigation techniques, just in case the ship's GPS had problems.
Astronomical Coordinate Systems
Like the explorers and thinkers who developed our terrestrial grid system of latitude and longitude, astronomers also use a grid system to define location—albeit with different axes, considering that they're describing the locations of objects on the sky rather than on Earth. Think how difficult it would be to explain where exactly something appears on the sky without using a grid system. All you could ever hope to do is give someone a general idea where to look, and hope they notice the same object you have in mind. In fact, in astronomy, we have different coordinate systems from which to choose, depending on how we want to describe the location of something. But there are natural coordinate systems that make intuitive sense to us as observers on Earth, and which we therefore might prefer to use.
In every grid system used to observe and map the sky, we start by imagining the sky as a spherical dome and project the coordinate axes outward onto the dome. One commonly-used grid system (the Equatorial Celestial Reference System) uses axes on which we measure positions called declination and right ascension; the intersection of these two coordinates (expressed in terms hours, arc-minutes, and arc-seconds) is where we find a particular object. The axes originate from the Earth's orbit around the Sun (defining what we call the ecliptic) and from the Earth's own rotation: that is, the poles and equator, from which we define north and south celestial poles and a celestial equator. In this system, declination can be thought of as similar to the concept of latitude (how high up is the object?), and right ascension can be thought of as similar to longitude (how far in this or that lateral direction?). Declination and right ascension, although somewhat akin to latitude and longitude, are not exactly the same as those concepts. If you want to learn more about them, a good introductory description can be found in Part 4 of H.A. Rey’s The Stars.
What Astrometry Measures
Astrometry seeks to make a highly precise two-dimensional map of the sky, and so it leaves out the dimension we think of as depth. We don't use astrometry to measure how far away things are from us, or how far away they might be from each other in that third dimension. To make the two-dimensional map, astrometry starts by imagining the sky as projected onto the inside of a spherical shell with a constant radius, as if Earth were at the center of a giant planetarium. Then, looking outward from Earth, astrometry measures how far apart the astronomical objects are from each other on the inside of the sphere. We call this the "separation on the sky" between two astronomical objects as we see them through our telescope on Earth.
If you've seen the night sky from the northern hemisphere, then you're probably familiar with the constellation Cassiopeia—the one that looks like a warped letter "W." (Anytime we talk about constellations, it's useful to remember the stars making up a constellation in all likelihood aren't actually near one another; they just look that way to us, on Earth. To alien astronomers on their home planet, those same stars would look very different.) The two brightest stars in Cassiopeia, as seen from Earth, are shown below. From other types of astronomical observations, as we’ll explain in a future blog entry, we’ve learned the brightest star in Cassiopeia is four times farther from Earth than the next brightest star. But that's completely independent of exactly what position each of those stars occupies on the dome of the night sky, or how far apart those same two stars appear from one another on that dome. On the inside of the dome, the two stars have certain locations, and a certain separation, both of which we can measure and watch over time to see how they change.
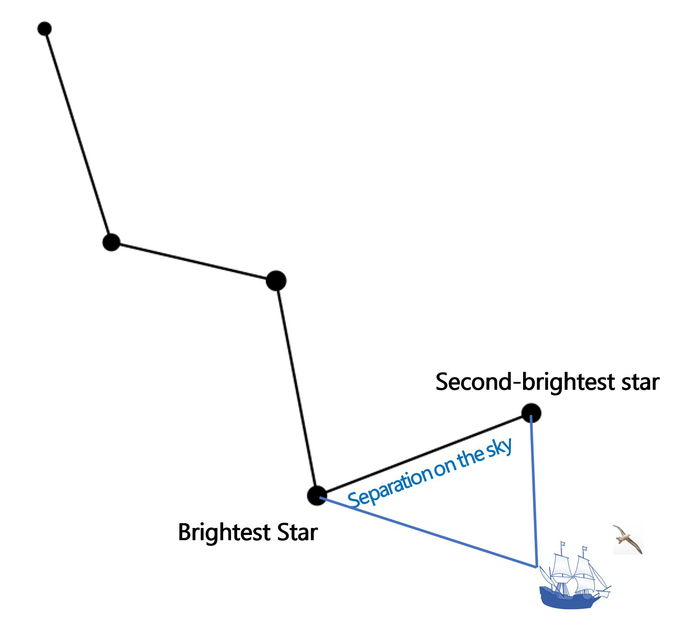
The two brightest stars of the constellation Cassiopeia, as seen from Earth.
Constellation Image Credit: Adapted from Dirk Hünniger/Wikimedia Commons Sailing Ship Image Credit: Adapted from Con-struct/Wikimedia Commons Albatross Image Credit: Nomis-simon/Wikimedia Commons
Why Astrometry Matters
You may wonder why astrometry is important to science. The simple answer is we want to know what's out there and where to find it. But beyond that, unless we have a good understanding of exactly what objects are located precisely where in the sky, and how they're moving, it's hard to learn the properties of those objects or know for sure if we're looking at something new. Conversely, when we do know those details, then we can learn surprising things about the cosmos that open doors to exciting new discoveries.
Astrometry has helped us understand things even about the makeup of our own Solar System, like finding the (former) planet Pluto. When astronomers were tracking Neptune's orbit around our Sun, they noticed a difference from what was expected. They wondered if maybe another, as-yet-undiscovered planetary body was out there, and used the orbital wobble of Neptune to locate that mysterious planetary body: Pluto. (Pluto is, of course, no longer considered a planet. At Caltech, I had the pleasure of studying planetary science with Professor Mike Brown, author of How I Killed Pluto and Why It had It Coming, and one of the researchers looking for a new Planet 9 out there.)
Astrometry has also been key to unlocking the secrets of exoplanets—including planets that might harbor life—black holes, and dark matter. One way astronomers can tell a planet is going around another star is by noticing its effects on the star's movement. And they can detect black holes by noticing their gravitational effects on the motions of nearby objects. In fact, we discovered a supermassive black hole at the center of our own Milky Way galaxy by carefully tracking the orbits of stars near the galactic center. Similarly, this kind of observation was also what led to the idea of dark matter: no one has ever actually seen dark matter, but something out there has mass, which affects the movements of other objects in ways we've observed through astrometry—and so we called that something dark matter. All of these things require that astronomers be able to notice and track small changes in the positions of the objects in the sky. In other words, they require astrometry.
Now that you're familiar with what astrometry is and why it's important, you'll probably want to know more about how we go about making these precise measurements. In Part 2 of this article, we'll look at some of the interesting challenges of astrometry and how TMT is preparing to meet them.
References
Samuel Taylor Coleridge, “The Rime of the Ancient Mariner”, annotated edition with an introduction and notes by Martin Gardner ; illustrated by Gustave Doré. Prometheus: New York (2003). See in particular pp.66-67 for elaboration on the extract included in this blog entry.
Andrew K. Johnston, Carlene E. Stephens, Paul E. Ceruzzi, and Roger D. Connor, “Time and Navigation: The Untold Story of Getting from Here to There”. Smithsonian Books: Washington, D.C. (2015)
H.A. Rey, “The Stars”. Houghton Mifflin Harcourt: Boston (1982)
Peter Barber, Ed., “The Map Book”. Walker & Company: New York (2005)
Dava Sobel, “Longitude: The True Story of a Lone Genius Who Solved the Greatest Scientific Problem of His Time”. Walker & Company: New York (1995)
Acknowledgement
Many thanks to my colleague Matthias Schöck, TMT System Scientist, for helping with this blog entry.


